- Introducción.
- Coeficiente de absorción.
- Absorción en un local.
- Nivel de presión sonora en un campo difuso.
- Tiempo de reverberación.
- Ecuación de Norris-Eyring.
- Medida del coeficiente de absorción.
- Campo sonoro en locales cerrados.
INTRODUCCIÓN.
En acústica, se conoce como absorción la energía de las ondas sonoras que al contactar en la superficie de cualquier material entra en el mismo en lugar de rebotar o ser reflectada. Los materiales se clasifican en función de su capacidad para absorber el ruido. Cuando una onda sonora atraviesa el aire se produce una absorción de la misma debido a la viscosidad y a la acción molecular del aire. En total, esta absorción es pequeña, excepto para altas frecuencias y largas distancias o habitaciones muy grandes. En las habitaciones son las superficies las que producen la absorción del sonido, bien mediante un proceso interno de extinción del sonido, o permitiendo el paso a través de ella. Un ejemplo extremo de este último tipo de absorción es una ventana abierta, ya que, aunque, en sentido absoluto la energía de la onda no se ha disipado, ha abandonado la habitación y puede considerarse como energía absorbida. La manera más sencilla de definir la absorción del sonido de una superficie es mediante un coeficiente que dé la relación entre la energía absorbida y la energía incidente.
COEFICIENTE DE ABSORCIÓN.
El coeficiente de absorción de una superficie se define como la relación entre la energía absorbida y la energía incidente. Normalmente, se expresa en Sabines dentro de una escala de 0 a 1. Su valor puede variar desde 1.0 para una ventana abierta, hasta 0.001 para una superficie muy pulida, como puede ser un enlucido de yeso pintado. En el coeficiente de absorción, en función de la frecuencia y para cada frecuencia, se pueden considerar dos coeficientes. Uno será el coeficiente de absorción de la onda normal,  0, que es fácil de medir. El otro será el coeficiente de absorción fortuito,
0, que es fácil de medir. El otro será el coeficiente de absorción fortuito,  , que indica las características acústicas de la habitación, por lo que se supondrá que las ondas sonoras golpearan la superficie con todos los ángulos posibles de incidencia. Es decir,
, que indica las características acústicas de la habitación, por lo que se supondrá que las ondas sonoras golpearan la superficie con todos los ángulos posibles de incidencia. Es decir,  , es independiente del ángulo de incidencia, sólo depende de la frecuencia,
, es independiente del ángulo de incidencia, sólo depende de la frecuencia,  puede medirse directamente o bien deducirse de
puede medirse directamente o bien deducirse de  0 haciendo algunas suposiciones.
0 haciendo algunas suposiciones.
El coeficiente normal de absorción,  0, puede obtenerse fácilmente a partir de una onda estacionaria. Su valor, cuando lo obtenemos teóricamente haciendo uso de la impedancia acústica de superficie ( Zs ), viene dado por la expresión:
0, puede obtenerse fácilmente a partir de una onda estacionaria. Su valor, cuando lo obtenemos teóricamente haciendo uso de la impedancia acústica de superficie ( Zs ), viene dado por la expresión:
 (1)
(1)
 Alcanza su valor máximo cuando Zs es real y Zs cos
Alcanza su valor máximo cuando Zs es real y Zs cos 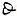 = Z0, pero esto sólo sucede para un valor de
= Z0, pero esto sólo sucede para un valor de 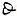 y sólo si Zs > Z0. En general, la variación de
y sólo si Zs > Z0. En general, la variación de  0 con el ángulo es una curva semejante a la de la figura de la izquierda.
0 con el ángulo es una curva semejante a la de la figura de la izquierda.
Normalmente lo que interesa es conocer el coeficiente de absorción fortuito ( ), es decir, el efecto absorbente de una superficie cuando está sometida al choque de ondas sonoras con varios ángulos de incidencia. Este coeficiente podemos obtenerlo integrando la energía absorbida con respecto a
), es decir, el efecto absorbente de una superficie cuando está sometida al choque de ondas sonoras con varios ángulos de incidencia. Este coeficiente podemos obtenerlo integrando la energía absorbida con respecto a 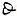 y dividiéndola por la energía total incidente.
y dividiéndola por la energía total incidente.

que teniendo en cuenta el valor de I0 puede transformase en:

donde  0 viene dado por la expresión (1).
0 viene dado por la expresión (1).
 En la figura de la izquierda se representa el valor del coeficiente
En la figura de la izquierda se representa el valor del coeficiente  en función del coeficiente de incidencia normal
en función del coeficiente de incidencia normal  0.
0.
ABSORCION EN UN LOCAL.
Si se considera el caso de una fuente sonora en el interior de un local, en cualquier punto del mismo, el nivel de presión sonora existente será el resultado de la suma de ondas sonoras que han sufrido una o varias reflexiones en las paredes del local.
A medida que nos alejamos de la fuente sonora, disminuye la intensidad de las ondas directas y es posible llegar a una zona en la cual el nivel sonoro resultante se debe prácticamente a las ondas reflejadas. Esta zona es el campo difuso que se caracteriza por ser no direccional, ya que las ondas viajan en cualquier dirección con igual probabilidad. Por estar en zona de campo difuso, todos los puntos del espacio tendrán el mismo nivel de presión sonora, ya que al ser ocasionado por las ondas reflejadas, todos lo puntos tienen la misma posibilidad de ser atravesados por las mismas ondas.
Para caracterizar este tipo de campo se utiliza el concepto de densidad de energía sonora, definida como la energía contenida en la unidad de volumen debida al movimiento vibratorio de las partículas del aire. Su unidad es el julio/ m³ y su valor viene dado por la expresión:
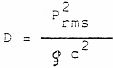 (1)
(1)
Suponiendo que la presión sonora es uniforme en todo el local, incluso cerca de las paredes, el balance de energía podrá representarse mediante la siguiente ecuación diferencial:
 (2)
(2)
donde:
V = volumen del local en m³.
D = densidad de energía sonora en jul/m³.
Er = energía radiada por la fuente en jul/seg.
Ea = energía absorbida por las paredes en jul/seg.
La energía absorbida por las paredes puede expresarse en función del coeficiente de absorción de las mismas:
 (3)
(3)
siendo:
I = intensidad sonora en jul/m² seg.
Si = área de la superficie “i” en m².
 i = coeficiente de absorción de la superficie “i”.
i = coeficiente de absorción de la superficie “i”.
El término ∑ Si  i tiene dimensiones de superficie y equivale al área necesaria de un material con coeficiente de absorción unidad para obtener la absorción del local. Se llama área de absorción o constante del local y se puede designar por R. Como
i tiene dimensiones de superficie y equivale al área necesaria de un material con coeficiente de absorción unidad para obtener la absorción del local. Se llama área de absorción o constante del local y se puede designar por R. Como  i es función de la frecuencia, también lo será el valor de R; por tanto, es necesario especificar la frecuencia para la que se ha calculado o medido R.
i es función de la frecuencia, también lo será el valor de R; por tanto, es necesario especificar la frecuencia para la que se ha calculado o medido R.
La intensidad sonora está relacionada con densidad de energía sonora a través de la ecuación:

Luego la expresión (3), que nos da la energía absorbida, puede escribirse en la forma
 (4)
(4)
Llevando este valor a la expresión (2), la ecuación de balance energético puede escribirse en la forma:
 (5)
(5)
cuya solución, sin definir de forma exacta Er, será:
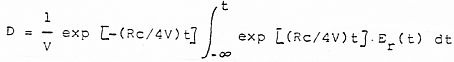 (6)
(6)
Debido a la exponencial dentro de la integral, la densidad de energía en cualquier instante, t, sólo depende del comportamiento de Er (t) en 4V/Rc segundos inmediatamente antes a dicho instante.
Si Er (t) es constante durante un periodo superior a 4V / Rc segundos, entonces la solución (6) será:
 (7)
(7)
y la Pr m s vendrá dada por:
 (8)
(8)
Se puede observar en este caso que la densidad de energía es constante en el interior de la habitación e inversamente proporcional a la absorción total.
Se ha de señalar que en R, solamente se ha incluido la absorción debida a las superficies del local. También se ha de incluir la debida a los objetos y personas contenidas en él. Para estos elementos, en vez de un coeficiente de absorción se suele dar directamente el área de absorción (A j = S j ∙  ). Incluyendo esta área en R tenemos:
). Incluyendo esta área en R tenemos:
 (9)
(9)
La tabla siguiente da la absorción del sonido por personas, medida en superficie equivalente, es decir, el producto S  .
.
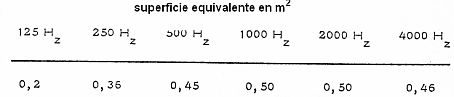
En el caso en que la fuente sonora comience inesperadamente en el tiempo t = 0, la solución (6) de la ecuación (5) pasa a ser:
 (10)
(10)
y si la fuente de sonido se detiene repentinamente en el tiempo t = 0, entonces la solución será:
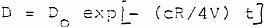 (11)
(11)
Así por ejemplo, la respuesta de una habitación a una sucesión de impulsos cortos (sílabas individuales cuando alguien habla) viene dada por las ecuaciones (10) y (11). El efecto de la habitación es sobreponer los impulsos y se llama falta de articulación. Si los impulsos se producen a intervalos fijos, el total del amontonamiento depende de la relación R/V que aparece en las funciones exponenciales de las soluciones (10) y (11). A medida que disminuye la absorción y se incrementa la longitud de la habitación los impulsos tienden a sobreponerse unos a otros.
NIVEL DE PRESIÓN SONORA EN UN CAMPO DIFUSO.
Si se considera que la energía sonora radiada por la fuente sonora es constante, o bien que es constante en un tiempo superior a 4V/cR. En este caso la solución a la ecuación del balance de energía sonora de la habitación viene dada por la expresión (7) del apartado anterior, es decir:
D = 4 Er / cR
donde: Er = energía radiada por la fuente sonora.
c = velocidad de propagación.
R = constante del local.
D = densidad de energía sonora.
Teniendo en cuenta la relación entre la densidad de energía sonora y la presión sonora cuadrática media, la ecuación (1) del apartado anterior, ose obtiene:

A partir de esta expresión podemos calcular el nivel de presión sonora. Para ello tomaremos para el producto “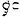 ” el valor 400 Kg/m² y una presión de referencia de
” el valor 400 Kg/m² y una presión de referencia de  . En estas condiciones, el nivel de presión sonora expresado en dB viene dado por:
. En estas condiciones, el nivel de presión sonora expresado en dB viene dado por:

donde: Lp = nivel de presión sonora.
Lw = nivel de potencia sonora de la fuente.
R = constante del local.
La expresión (1) nos dice que el nivel de presión sonora de un campo difuso es constante y sólo depende de la potencia de la fuente y de la absorción del local.
Conviene señalar que para obtener la expresión (1) se ha supuesto que la presión era uniforme en todo el local, a pesar de esto la ecuación es correcta para aplicaciones prácticas y la mayoría de los autores la recomiendan para estos fines, determinando el valor de R con los coeficientes de absorción de Sabine.
TIEMPO DE REVERBERACION.
El hecho de que la energía sonora disminuya exponencialmente cuando la fuente sonora se detiene, se denomina reverberación. Una medida de este fenómeno indicará la mayor o menor absorción del local.
En orden a determinar cuantitativamente la reverberación de un local, se define el tiempo de reverberación cómo, “el tiempo que es necesario dejar transcurrir desde el instante en que la fuente sonora deja de actuar, hasta que la intensidad se reduce a la millonésima parte de su valor inicial”, es decir, una disminución de 60 dB.
Suponiendo inexistente la absorción del aire, esta definición puede aplicarse a la ecuación (11) del apartado “Absorción de un local” y así resulta:

donde: T será el tiempo de reverberación.
Tomando logaritmos resulta:

de donde:
 (1)
(1)
Esta ecuación (1) no tiene dimensiones, pero normalmente se sustituye el valor de la velocidad del sonido (c), en pies por segundo o en metros por segundo. Dicha ecuación se conoce con el nombre de ecuación o ley de Sabine que adopta las dos expresiones siguientes:
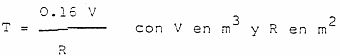
La ecuación de Sabine permite medir experimentalmente el valor de R a partir de medidas del tiempo de reverberación, que a su vez son utilizadas para la determinación en laboratorio de los coeficientes de absorción.
Teniendo en cuenta la absorción debida al aire, entonces la ecuación (1) pasa a ser:
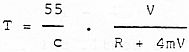
Donde m es la constante de atenuación de energía para el aire.
ECUACION DE NORRIS – EYRING.
La ley de Sabine sólo puede aplicarse para los casos límite en que la superficie total de la habitación es pequeña. Si el cociente medio de absorción de todas las superficies es dado por:

donde S es la superficie total, es mayor de 0´1, por lo que entonces es más exacto utilizar la ecuación de Norris – Eyring, que a continuación se expone, que es la ley de Sabine para la determinación del tiempo de reverberación.
Si se supone un local en cuyo interior hay una fuente sonrosa. Al incidir la energía radiada sobre las paredes del local, ésta se refleja, sufriendo la intensidad una reducción en la proporción  m, siendo
m, siendo  el coeficiente medio de absorción definido en la ecuación (1) después de n reflexiones, la intensidad remanente será:
el coeficiente medio de absorción definido en la ecuación (1) después de n reflexiones, la intensidad remanente será:

El camino libre medio de las ondas sonoras es 4V/s por lo que tendremos Sct / 4V reflexiones al cabo de un tiempo medio “t”. Entonces, la intensidad remanente será:
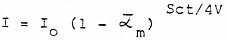
Utilizando ahora la definición de tiempo de reverberación T, es decir, el necesario para que la intensidad decrezca hasta  tenemos:
tenemos:

Tomando logaritmos decimales y despejando el valor de T, resulta:
 (2)
(2)
que se conoce con el nombre de ecuación de Norris –Euring. También se puede escribir, teniendo presente el valor de  m, en la forma:
m, en la forma:
 (3)
(3) 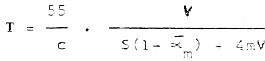
o bien:

 (1)
(1) 1 la nueva área equivalente será:
1 la nueva área equivalente será:
 (2)
(2)
y el nuevo tiempo de reverberación:

Llevando a esta expresión el valor de A1 dado por la igualdad (2) y despejando  1, teniendo presenta la igualdad (1), se tiene que:
1, teniendo presenta la igualdad (1), se tiene que:

 1 superiores a la unidad, debido a que se está usando la ecuación de Sabine en unas condiciones que verifican las hipótesis en su deducción.
1 superiores a la unidad, debido a que se está usando la ecuación de Sabine en unas condiciones que verifican las hipótesis en su deducción.
A pesar de este inconveniente este método de medida del coeficiente de absorción es muy utilizado, si bien el coeficiente de absorción que se obtiene se designa por  SAB para distinguirlo del
SAB para distinguirlo del  teórico.
teórico.
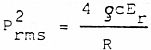 (1)
(1)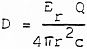 (2)
(2)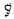 = densidad del aire.
= densidad del aire.El factor Q se define como el cociente entre la energía radiada en una dirección y la que se radiaría en esa dirección si la fuente fuese omnidireccional y de la misma potencia.
Teniendo en cuenta la relación existente entre la presión sonora eficaz y la densidad de energía (ecuación (1)) la presión sonora debida al campo directo valdrá:

Sumando a esta presión la correspondiente al campo difuso (ecuación (8) del apartado Absorción en un loca, se obtendrá la presión sonora total.

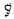 c el valor de 400 Kg/m²/seg.
c el valor de 400 Kg/m²/seg.
En estas condiciones dicho nivel vale:

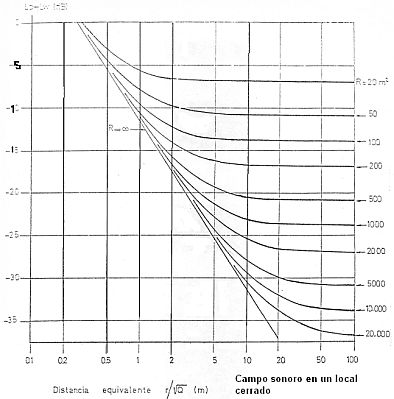
Analizando esta figura queda claro que un tratamiento del local consistente en aumentar el área de absorción, sólo reducirá el ruido en lugares alejados de la fuente sonora. La cuantificación de este hecho nos lleva al concepto de distancia crítica que se define como la distancia a la fuente sonora a partir de la cual un aumento de la absorción del local se manifiesta en una reducción del ruido. Dicha distancia se puede estimar en la ecuación:

siendo: r = Distancia crítica en m.
R = Constante del local en m².
Q = Directividad de la fuente sonora.
Una norma práctica que es muy útil para las primeras evaluaciones de posibilidades de reducción de ruido, es considerar como campo directo de una máquina, el volumen de un cono con el centro de la base en la máquina, el vértice en el techo y radio de la base igual a su altura. En el interior de este volumen no son posibles reducciones de ruido si no es con absorbentes aplicados en superficies fuera de él. En conclusión, el uso de recubrimientos absorbentes sólo es efectivo en locales con un gran tiempo de reverberación y en zonas alejadas de las fuentes de ruido.
