Cuando se realiza una instalación en la que van a estar instaladas fuentes sonoras se ha de estimar el nivel de ruido que cabe esperar tanto en puntos del interior de la instalación, donde las personas u operarios pueden encontrarse expuestas al mismo, como en puntos exteriores a la instalación donde las exigencias urbanísticas pueden establecer unos niveles sonoros máximos. Para hacer frente a esta necesidad es imprescindible estudiar las fuentes sonoras como manantial de potencia acústica con su espectro correspondiente. Luego se han de analizar los mecanismos de propagación de las ondas en el espacio real donde se producen los fenómenos de aislamiento por obstáculos y absorción por superficies, lo que condiciona el nivel sonoro. Posteriormente se darán las guías para el cálculo del nivel sonoro en los puntos del interior de la instalación y se presentará un procedimiento para la estimación del nivel en puntos exteriores a la misma.
FUENTES SONORAS. Durante la fase de proyecto de una instalación nueva o de remodelación de una ya existente, es cuando se dispone de mayor oportunidad para evitar niveles sonoros elevados. En algunos casos las características acústicas de las fuentes pueden determinarse por vía experimental, o en su defecto estimarse teóricamente, aunque siempre son preferibles las estimaciones experimentales, aunque sean mediocres, a las estimaciones teóricas. De las características acústicas de la fuente, lo más importante es conocer su emisión sonora distribuida espectralmente, bien en bandas de octava o de tercios de octava y de sus características direccionales. El conocimiento de la distribución espectral de la potencia sonora presenta cierta complejidad técnica. Por ello en su lugar se recurre a la distribución espectral de nivel de presión sonora, que por supuesto dependerá del punto que se elija y de las características direccionales de la fuente. Por ello es conveniente que las características de las fuentes estén determinadas siguiendo unas normas bien definidas con objeto de evitar errores de interpretación de resultados. En algunos casos, cuando no se disponen de datos experimentales, es posible estimar el ruido que generan algunas máquinas o equipos mediante expresiones semiempíricas que permiten determinar los valores aproximados.
Ventiladores. Para el cálculo del espectro de potencia sonora de un ventilador se parte del nivel de potencia de un ventilador del mismo tipo trabajando en condiciones normalizadas (caudal de 1 m³ / h a un incremento de presión de 1 cm de agua) a partir de este dato se calcula el espectro real acudiendo a la siguiente ecuación: donde: Lw = Nivel de potencia sonora real (dB referidos 10 -¹² watt). LB = Nivel de potencia normalizado (dB referidos 10 ¹² watt). Q = Caudal (m³ / h) ΔP = Incremento de presión (cm H2O) Existen tablas con los espectros de potencia normalizados, como esta:
En la banda correspondiente a la frecuencia de paso de las palas del ventilador deben añadir algunos dB, incremento que viene dado en la tabla superior. La frecuencia de paso de las palas es: f b = V . N 60
donde: f b = Frecuencia del paso de las palas (Hz). V = Velocidad de giro del rodete (rpm). N = Número de palas. El espectro así calculado responde al total de la energía radiada, y se debe restar 3 dB para estimar el ruido que sale por aberturas de aspiración y descarga.
Bombas. El espectro de frecuencias es muy variable, ya que dependerá de las estructuras que entre en vibración inducido por la bomba. Cuando no se dispone de datos experimentales el nivel de potencias se puede estimar por la ecuación: Lw = 97 + 10 log P(1 – e/2)
donde: P = Potencia hidráulica de la bomba (HP) e = eficiencia de la bomba. El espectro se puede considerar plano con la presencia de alguna banda predominante.
Compresores. Se han de diferenciar los compresores centrífugos en los que la potencia acústica depende de la potencia y de la velocidad del rotor y los compresores tubulares para los que la potencia sonora solamente depende de la potencia.
Compresores centrífugos: el nivel de potencia sonora se pude determinar mediante la ecuación: Lw = 20 log P + 50 U - 38
donde: P = Potencia del compresor (NP). U = Velocidad periférica del rotor (m/s). El espectro presenta un máximo en la frecuencia: f = 4,1 U
Compresor tubular: el nivel de potencia global viene dado por: Lw = 76 + 20 log P. donde su máximo es el segundo armónico de la frecuencia de paso de las palas, o sea: f = 2 NV 60 donde: N = número de palas. V = Velocidad de giro del rotor (rpm)
Chorros de aire. El ruido producido por la descarga de un chorro de aire a la atmósfera es muy elevado y el nivel de potencia sonora se puede estimar por la expresión: Lw = 80 log v + 20 log d - 114
donde: v = velocidad de descarga (m/seg). d = diámetro del tubo de descarga (mm). El nivel de presión sonora en un punto dependerá además de la potencia sonora de la distancia al choro y de la directividad del mismo. Puede estimarse por la ecuación: Lp = Lw - 11 + DI - 20 log r
donde: DI = corrección de directividad. r = distancia entre el punto y el chorro (m). La corrección de directividad se encuentra en la tabla siguiente en función del ángulo que forma el eje del chorro con la recta que une el punto de descarga y el de medida. La corrección de directividad se encuentra en la tabla siguiente en función del ángulo que forma el eje del chorro con la recta que une el punto de descarga y el de medida.
El espectro es bastante plano y presenta un máximo a la frecuencia: Fo = 130 v d
donde: v = velocidad de salida del aire (m/seg). d = diámetro de la boquilla (mm) Para el cálculo del espectro se puede utilizar la tabla siguiente en la que se expresan las correcciones a aplicar a nivel global para el cálculo del espectro sonoro.
En esta tabla se dan los espectros sonoros para distintas fuentes sonoras.
PROPAGACION DEL SONIDO. En la propagación del sonido desde la fuente hasta el receptor se presentan una serie de fenómenos que se pueden clasificar en tres grupos: a) Transmisión de las ondas aéreas desde la fuente al receptor. Esta transmisión puede quedar amortiguada por interposición de obstáculos en el trayecto. Esta técnica se conoce como aislamiento del sonido aerotransportado. b)Transmisión de las ondas a través de las estructuras de los edificios, desde los cuales se irradiarán ondas. Esta propagación se puede producir con estructuras poco transmisoras o evitando que las vibraciones alcancen la estructuras. c) Reflexión de ondas en las superficies sólidas del local. Transmisión que puede reducirse mediante materiales absorbentes que disminuyen las reflexiones del sonido.
AISLAMIENTO. Se entiende por aislamiento acústico a la protección de un recinto contra la penetración de sonidos que interfieran la actividad que se desea realizar, o bien para evitar que altos niveles de presión sonora generados en el interior puedan salir al exterior o pasar a terceros recintos en que no son deseables. Lo primero a tener en cuenta es que las fuentes que originan estos ruidos pueden estar dentro o fuera del recinto que pretendemos aislar, y lógicamente el enfoque será diferente como se verá más adelante. Así, lo primero que se debe establecer es la naturaleza de los ruidos que existan y los caminos de entrada al recinto a través de sus superficies límite y si no se puede reducir la fuente de ruido, la única alternativa es evitar que su efecto llegue a los oídos. Se consigue mediante la interposición de obstáculo sólido, no poroso, al paso de la onda sonora. Cuando la onda sonora actúa sobre la superficie del obstáculo, la variación de presión origina una fuerza que la pone en vibración apareciendo al otro lado del obstáculo un nuevo foco de generación de onda. En las paredes se puede colocar materiales de absorción acústica y se pueden situar estratégicamente paneles que absorbentes para reducir las reflexiones. Pero todas estas reflexiones son sólo útiles para las personas que no están en las proximidades de la fuente sonora.
El primer paso para diseñar una envoltura es realizar un análisis en octavas del ruido producido por la fuente. Esto exige, a veces, poner en funcionamiento la fuente ruido (máquina), en ausencia de otras fuentes perturbadoras. El segundo paso consiste en calcular los cambios espectrales necesarios para reducir el ruido a un nivel aceptable. Y al final en diseñar la envoltura cuyas características aislantes proporcionan los cambios espectrales necesarios. Realizada la instalación, se puede usar un sonómetro con filtros de octava para probar la eficacia del sistema. El aislamiento proporcionado por un obstáculo se expresa por el coeficiente de transmisión como cociente entre la energía transmitida por el obstáculo y la incidente en el lado opuesto.
Coeficiente de transmisión T = energía transmitida energía incidente Es de uso más corriente el índice de aislamiento que expresa la diferencia del nivel sonoro a ambos lados del obstáculo y viene expresado en dB Indice de aislamiento = 10 log 1 dB = A T
Frecuencia crítica. La onda sonora en el aire es una onda longitudinal y su velocidad es independiente de la frecuencia de la vibración. Sin embargo, la propagación de las vibraciones mecánicas en un sólido puede efectuarse por otros tipos de ondas. En el caso que nos ocupa, paredes delgadas, las vibraciones mecánicas se transmiten principalmente por ondas de flexión por lo tanto transversalmente. En este tipo de ondas la velocidad de propagación depende de las características mecánicas de la pared y de la frecuencia de las vibraciones. La velocidad de la onda de flexión en pared viene dada por: donde: E = módulo de Young. t = espesor. f = frecuencia. Por tanto aumenta con el espesor y la frecuencia. La frecuencia para la cual la velocidad de propagación de una onda de flexión es igual a la velocidad del sonido en el aire se la denomina frecuencia crítica, que depende de la densidad de la pared, del espesor de la misma y de sus características elásticas. Por ello se denomina característica de un material al producto de su frecuencia crítica por la densidad superficial.
Aislamiento proporcionado por paredes simples. Se entiende por pared simple o de una sola capa aquella en que los puntos de la masa que están sobre la misma normal no modifican su distancia mutua cuando la pared realiza vibraciones. Esta pared no tiene por qué ser homogénea, puede estar formada por varias capas y puede contener también huecos. En el caso teórico más simple de una pared no porosa de dimensiones infinitas y delgada, el aislamiento sigue la ley teórica conocida como ley de masa. Es decir, que el aislamiento no de pende de las características absorbentes del material, sino de la ley de masa del aislamiento. Esta ley establece que cada vez que se duplica la frecuencia o la masa superficial de la pared, el aislamiento aumenta en 6 dB. Su expresión: A = 43 + 20 El aislamiento depende del ángulo de incidencia de la onda, siendo máxima para incidencia normal y mínima para rasante. Para los cálculos prácticos se consideran que las ondas inciden sobre la pared con igual intensidad entre – 80º y + 80º denominada incidencia práctica.
Esta ley es válida con gran aproximación para cualquier material sólido, no poroso de grandes dimensiones y de espesor suficientemente inferior a la longitud de onda. Sin embargo, no se cumple para todo el espectro de frecuencias, su campo de validez está delimitado por la frecuencia de resonancia de la pared, principalmente paredes pequeñas y por la frecuencia crítica que seguidamente se comenta. No obstante las frecuencias de resonancia son lo suficientemente bajas y por ello prácticamente no se tiene en cuenta a la hora de calcular aislamientos.
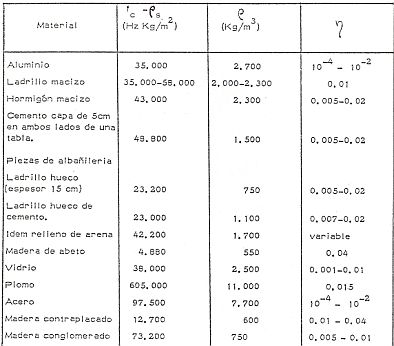
En la siguiente tabla se presentan los valores de productos s . f c para algunos materiales.
Cuando una onda aérea, incide en la pared y su frecuencia es iguala a la crítica del material, se produce un acoplamiento entre la onda aérea y la onda de flexión que ser forme en la pared, ya que se confunde en su velocidad y frecuencia. Esto haría que la transmisión por la pared fuese perfecta a no ser por las pérdidas debidas al rozamiento en el interior del sólido. Este acoplamiento se daría si la onda aérea incidiese paralelamente a la pared, incidencia poco probable. Sin embargo, para incidencias superiores a la crítica, siempre hay un ángulo de incidencia para el cual los frentes de ondas aéreas alcanzan la pared a distancias iguales a la longitud de onda de la onda de flexión, coincidencia que favorece la trasmisión y por lo tanto debilita el aislamiento. Para frecuencias superiores a la crítica, se produce un debilitamiento del aislamiento que no es fácil predecir ya que es función de las propiedades internas de rozamiento difícilmente estimables. No obstante, estas pérdidas pueden cuantificarse aproximadamente en función del denominado factor de pérdidas. El factor de pérdidas es propio para cada material y en función de él puede estimarse la diferencia de aislamiento que se produciría a frecuencias superiores a la crítica.
Una pared simple vendrá determinada por su característico s . f c y su factor de pérdidas ŋ. En función de estos valores puede determinarse el aislamiento en la forma siguiente. El aislamiento es función de la frecuencia, por ello se tendrá que determinar el espectro del aislamiento, pudiendo calcularse aplicando la expresión siguiente: donde: A (f)= aislamiento a una frecuencia. A /fc)= asilamiento a la frecuencia crítica suponiendo que se cumpliera la Ley de masa. Así por ejemplo si se quiere determinar el aislamiento proporcionada por una placa de aluminio de 1,5 x 2 m. De superficie y de 1/8 de pulgada de espesor. Los cálculos a realizar serán los siguientes: Espesor d= 1/8 de pulgada= 3´17 mm. Densidad superficial: Frecuencia crítica:
Factor de pérdidas: ŋ = 0´01 Aislamiento a la frecuencia crítica, es decir a 35.000 Hz Kg / m², tomando la Ley de masa:44 dB. La determinación del espectro de aislamiento se ha de realizar siguiendo los datos de la figura de la arriba, con los que se construye la tabla siguiente.
Frecuencia de resonancia. Esta solo tiene validez para paredes de pequeñas dimensiones. Se puede observar que a bajas frecuencias generalmente inferiores a 100-200 Hz existe una discrepancia entre el aislamiento estimado por la Ley de masa y los valores experimentales. Discrepancia que es debida a los efectos de resonancia de la propia pared con la onda de flexión. Esto se traduce en una disminución de aislamiento a esta frecuencia y a sus armónicos. No obstante, a la hora de estimar la capacidad agresiva del ruido, este fenómeno tiene poca importancia, ya que las componentes de baja frecuencia presentan menor agresividad.
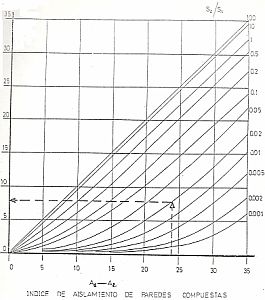
En la práctica con frecuencia se presentan paredes que están constituidas por distintos materiales, por ejemplo, paredes de ladrillo y superficie de ventana. En estos casos el índice de aislamiento es: donde: S1 = a superficie del material.
Para el caso de dos materiales la fórmula anterior se presenta normalizada en la figura de la izquierda, donde S 1 y S 2 son las superficies de cada material y A 1 y A 2 sus aislamientos respectivos.
Un método normalmente muy bueno de aumentar el aislamiento acústico de una pared, sin tener que aumentar de manera desorbitada su masa superficial, es recurrir al uso de paredes múltiples. Se divide la pared en un número de capas delgadas separadas por una cámara de aire de manera que el ruido se reduce por etapas. La estimación del aislamiento se basa en normas más o menos empíricas y con pocas garantías en sus resultados, ya que a la transmisión “pared, hueco, pared” se le asocia la transmisión por los puntos de unión de las paredes con el suelo y con las viguetas. En las figuras de la izquierda se presentan las diferencias de aislamiento de las paredes simple y hueca del mismo peso y el efecto de las uniones.
Ver en las figuras de la izquierda la influencia del absorbente en el hueco. Puede observarse el aislamiento medio proporcionado por una pared hueca en función del espesor del hueco y de la masa superficial. El incremento del aislamiento que se obtiene con el sistema de la pared doble es función de la anchura de la cámara de aire, del material de la placa y del número de uniones, consiguiendo un aislamiento entre 6 y 10 dB mayor que el conseguido por la pared del mismo peso.
Alojamiento del sonido transportado por la estructura. La vibración de la fuente puede ocasionar una serie de vibraciones mecánicas en la estructura que posteriormente pueden radiar energía sonora transformándose en nuevas fuentes sonoras. El ruido transportado por esta estructura se puede amortiguar: a)Evitando que la energía llegue a la estructura. b)Dificultando la transmisión de la onda a lo largo de la misma.
En la práctica esto puede conseguirse mediante el recubrimiento de suelos o con la utilización de suelos flotantes. El recubrimiento de suelos con materiales elásticos como goma o caucho, amortiguan los golpes y en consecuencia disminuyen la energía transmitida a la estructura. La eficacia de estos recubrimientos es buena para frecuencias altas (superiores a 1000 Hz), aunque su utilización no es posible en muchos casos. Un recubrimiento disminuye la emisión de ruido según: Δ Ln = log. f para f > f o fo donde: Δ Ln _ disminución del ruido emitido (dB) f = frecuencia del ruido (Hz). f o = frecuencia de resonancia (Hz) para f < fo Δ Ln = 0
La otra solución está proporcionada por los suelos flotantes que consisten en la separación del suelo rígido estructural de la base de la fuente de vibraciones. Se logra mediante la colocación de una capa de material elástico o una serie de bloques de goma separados, con la ventaja sobre el anterior método de ser más resistentes a la abrasión y de mejorar el aislamiento, tanto de los ruidos aéreos como de los golpes. El suelo flotante más simple se realiza colocando sobre el suelo estructural una capa de material elástico, se recubre con fieltro y sobre ésta se añade una capa de hormigón armado ligero, cuidando que el suelo flotante no haga contacto rígido con las paredes. Un poco más complejo es realizar un suelo flotante similar al anterior con introducción de una placa de rigidez suficiente para evitar que se agriete el suelo flotante. La capa elástica está formada por los soportes de goma sobre los que se apoya la placa. Los huecos entre soportes se rellenan con un absorbente. Por último se puede realizar un suelo flotante sobre estructura de madera.
Aislamiento de vibraciones. El efecto de transmisión por estructura se puede quedar reducido en gran manera si se evita que la vibración de una máquina se transmita al suelo, intercalando entre máquina y suelo un elemento de material elástico. El comportamiento de un amortiguador de vibración es similar al de un suelo flotante, por ello se ha de tener en cuenta la frecuencia de resonancia, que será tanto menor cuanto mayor sea la masa y elasticidad del amortiguador. Esta amortiguación es eficaz para frecuencias diez veces superiores a la frecuencia de resonancia. |
La solución más eficaz de asilamiento es la envoltura o pantalla antirruido en torno a la fuente sonora. Las envolturas deben de ser totalmente cerradas, porque incluso pequeñas fugas anulan totalmente su efecto. Por otro lado, el aislamiento de la fuente sonora no siempre es posible pues pueden surgir problemas de temperatura y de carga, que habrá que resolver, pero son sistemas muy eficaces de reducción del ruido.
= densidad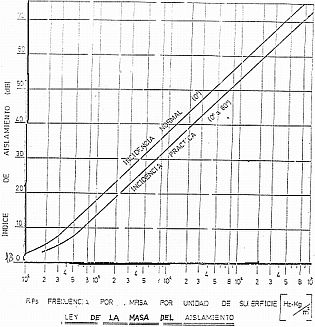
Cálculo de aislamiento de una pared simple.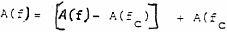
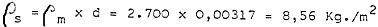
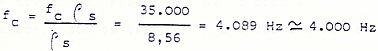
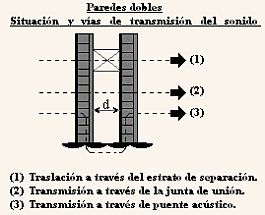Paredes dobles.
por ello, la efectividad de un recubrimiento aumenta cuando la frecuencia de resonancia es más baja, lo que se consigue al aumentar el espesor del recubrimiento. Generalmente la frecuencia de resonancia oscila entre 200 y 500 Hz.