- Psicofísica de la audición.
- Nivel sonoro en función de la frecuencia.
- Sensación sonora – sonoridad.
- La sonoridad en función de la anchura de banda.
- Influencia de la proximidad de las frecuencias en la sonoridad.
- Cálculo de la sonoridad de un ruido de banda ancha.
- Enmascaramiento.
- Simulación de la distribución del enmascaramiento en la membrana basilar.
- Cálculo de la sonoridad de un ruido de banda ancha.
PSICOFÍSICA DE LA AUDICIÓN.
La percepción sonora experimentada en los seres humanos abarca una serie de mecanismos fisiológicos y psicológicos muy complicados, siendo su conocimiento aún solamente empírico. Sin embargo, en la actualidad se construyen modelos de la función sensorial auditiva bastante aproximados y fiables. De aquí, que la evaluación de la sensación sonora es mucho más compleja que las simples medidas de las magnitudes, ya que el problema que se presenta exige el conocimiento de la relación entre los estímulos recibidos, que son magnitudes físicas, y las sensaciones originadas, que son magnitudes puramente subjetivas.
El primer intento en la búsqueda de la existencia de una relación entre el campo de los estímulos y el de las sensaciones fue realizado por Ernst Weber, quien constató que una persona no diferencia entre dos estímulos a menos que se diferencien en una proporción fija y mínima. Así, para el caso de la audición, el oído humano no diferencia intensidades entre dos sonidos que no se diferencien entre ellos al menos en un 25%. A este incremento es lo que luego denomina Weber diferencia mínima perceptible.
Posteriormente Gustav Fechner, basándose en los descubrimientos de Weber, realiza un intento de medir indirectamente las sensaciones, publicando en 1860 su obra Elementos de Sicofísica, en la que resume todo su trabajo en una ley matemática sencilla según la cual se podría valorar en magnitud la sensación producida por cualquier estímulo. Expresó esta ley de la forma siguiente: “al multiplicarse la intensidad de los estímulos, las sensaciones aumentan por adición”, o lo que es lo mismo, las sensaciones siguen la ley logarítmica de los estímulos. Para que un estímulo sea apenas diferenciable de otro que lo precedió, aquél debe de incrementarse en su intensidad en una proporción constante con respecto al estímulo original
En el caso de dos sonidos de intensidades I1 e Io, suponiendo que I1 > Io, la diferencia de las sensaciones producidas, haciendo uso de la ley anterior de Fechner, sería:
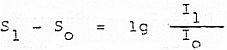
Si Io fuese la intensidad física umbral de la percepción, a la cual corresponde la sensación So = 0, la sensación sonora producida por el sonido de intensidad I1 sería:
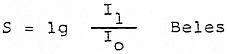
o bien:
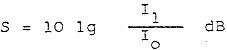
motivo por el cual se introdujo el dB para expresar magnitudes subjetivas.
En definitiva que como ya se expuso en el capítulo 06.2ª.01, la relación entre la magnitud del estímulo acústico y la magnitud de la sensación auditiva provocada, sigue la llamada ley de Weber-Fechner, según la cual las respuestas sensoriales a los estímulos varían como los logaritmos de esos estímulos.
No obstante, la sensación sonora no solamente depende de la intensidad física, sino también de la frecuencia de la vibración, y cuando se trata de un sonido complejo de la anchura de banda.
NIVEL SONORO EN FUNCIÓN DE LA FRECUENCIA.
Si la percepción del oído humano fuese independiente de la frecuencia, dos tonos puros de la misma intensidad física, producirían la misma sensación sonora. Sin embargo no es así, sino que la sensación sonora varía con la frecuencia.
Fletcher y Munson publicaron en 1953 las curvas isosónicas que ligeramente modificadas fueron adoptadas por la recomendación ISO-226.
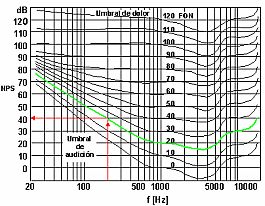
Este fenómeno del nivel sonoro en función de la frecuencia del sonido es fundamental en psicoacústica y ha creado la necesidad de utilizar otra unidad que expresa mejor la sensación sonora producida por un sonido de una determinada intensidad física, apareciendo así la unidad Fonio que se define como: “El valor numérico de la intensidad de cualquier ruido en fonios, es igual al valor numérico en dB del nivel de presión de un sonido de 1000 Hz que se perciba con la misma intensidad que el ruido considerado”.
Las curvas de isosónias representadas en la figura superior están obtenidas para un tono puro y campo frontal. Muestran, por ejemplo que un sonido a 100 Hz de frecuencia y de un nivel de presión de 50 dB, produce la misma sensación sonora que otro de 40 dB a 1000 Hz, o lo que es lo mismo, el ruido considerado será de 40 fonios.
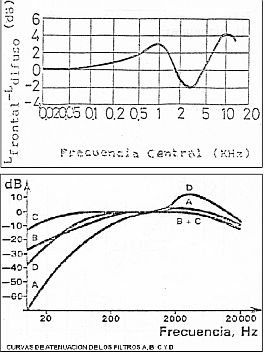En caso de un campo difuso, las curvas isosónicas presentan una pequeña desviación respecto a las representadas arriba. Esta desviación fue normalizada en la recomendación ISO-454, con la cual se determinan las curvas isosónicas en campo difuso a partir de las de campo plano.
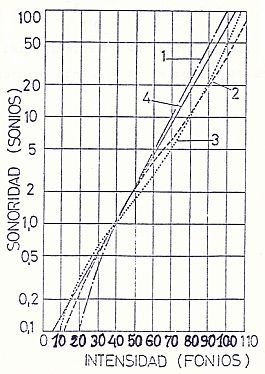
En base a la respuesta del oído humano a las distintas frecuencias parece que debería ser sencillo realizar un circuito electrónico cuya sensibilidad siguiera la misma ley que el oído humano. Como ya se ha expuesto en el capítulo anterior el resultado de este intento ha sido normalizado internacionalmente como los sistemas de ponderación o filtros A, B y C. El sistema “A” se aproxima a las curvas isosónicas de bajos niveles de presión; el sistema “B” a las de nivel medio y el filtro “C” a las de nivel alto.
Sin embargo, para estimar la capacidad agresiva de un ruido se ha impuesto la utilización del filtro “A”, que da una mejor correlación entre los niveles de presión acústica y sus efectos.
Últimamente se ha introducido la ponderación “D” para la medida del ruido de aviones a reacción.
Con respecto a la frecuenica existen comportamiento del sonido que pueden parecer sorprendentes, pero que tienen una explicación física. Un ejemplo de estos fenómenos es el efecto doppler (el sonido de una ambulancia) que es el aparente cambio de frecuencia de una onda producido por el movimiento relativo de la fuente respecto a su observador. La frecuencia de un sonido en el punto en que lo oye un observador varía en función de parámetros que dependen de la frecuencia del sonido en su fuente, de la velocidad del movil que lo produce y de la velocidad del sinido en el medio físico que se trata según la siguiente fórmula:
SENSACION SONORA – SONORIDAD.
El fonio, o fon, es una unidad de medida logarítmica y adimensional (similar al decibelio) que se usa para indicar la sonoridad con que se percibe un sonido dado. Si bien el fonio expresa el nivel sonoro, es evidente que la sonoridad de un ruido de 120 fonios no se aprecia como si tuviera doble sonoridad que otro ruido de 60 fonios, el primero es doloroso, mientras que el segundo es una cómoda conversación.
Con objeto de poder establecer una nueva escala que refleje mejor este hecho, los Psicofísicos de Harward fueron quienes utilizando el procedimiento llamado estimación de la magnitud sonora, dando origen a la escala llamada “Sone”, definiendo la unidad son como la sonoridad de un tono de 1000 Hz y 40 dB de nivel de presión.
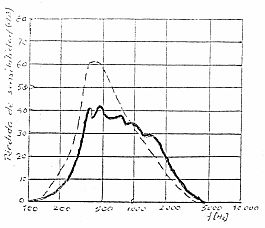
Las observaciones llevadas a cabo por Fletcher y Munson dieron por resultados la curva de la figura de la izquierda, según la cual en intensidades pequeñas una duplicación de la sonoridad corresponde a un aumento de 4 a 6 fonios y en intensidades grandes el salto viene a ser de 8 a 10 fonios. Las medidas más recientes de Awicker dan como resultado las curvas 2 y 3 de la figura. La recomendación ISP adopta una solución intermedia, que es la curva 4, según la cual una duplicación de la sonoridad corresponde a un salto de 10 fonios. Según esta norma la sonoridad puede calcularse por la expresión:
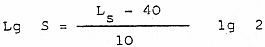
válida para niveles de 40 fonios o más, donde Ls es el nivel sonoro en fonios y S la sonoridad en sonios.
LA SONORIDAD EN FUNCION DE LA ANCHURA DE BANDA.
En el oído humano, los sonidos de banda ancha producen una sensación sonora más intensa que los tonos puros del mismo nivel de presión. Los estudios realizados vienen a confirmar que para cada frecuencia central queda definida una banda crítica, de forma que los sonidos de anchura inferior a ella y del mismo nivel producen la misma sensación sonora, existiendo un marcado aumento de la sonoridad cuando se supera dicha banda crítica.
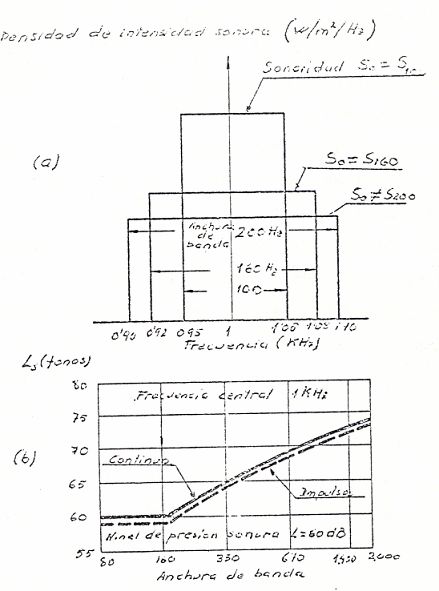
La figura inferior muestra este efecto para un ruido de banda limitada con frecuencia central de 1 KHz. En la parte superior (a) se representan tres sonidos de banda ancha de 100, 160 y 200 Hz. Los tres espectros definen la misma área, por lo que los tres sonidos tienen la misma intensidad sonora y por lo tanto el mismo nivel de presión. Sin embargo, el sonido de anchura de 200 Hz, presenta una sonoridad mayor. La parte inferior de la figura (b) muestra como influye el aumento de la anchura de banda en la sonoridad. Para sonidos de frecuencia central 1 KHz, la anchura crítica es 160 Hz, existiendo por encima de este valor un aumento lineal de la sonoridad.
Aunque para cada frecuencia central queda definida una banda crítica con gran aproximación entre las frecuencias 250 Hz y 14 KHz, los anchos de banda críticos pueden considerarse iguales a tercios de octava.
INFLUENCIA DE LA PROXIMIDAD DE LAS FRECUENCIAS EN LA SONORIDAD.
La escala de sonidos parece, en principio, que serviría para calcular directamente por adición la sonoridad producida por varios sonidos que actúan simultáneamente. Sin embargo, esto sería válido solamente si los dos sonidos estuvieran ampliamente separados en frecuencia. Así, por ejemplo, la sonoridad de dos tonos de 70 fonios y frecuencia 200-400 Hz cuando actúen simultáneamente, debido a la amplia separación de frecuencias, es la suma de las sonoridades individuales de cada uno de los dos. En este caso, como la sonoridad correspondiente a 70 fones es de 8 sonios, la sonoridad conjunta será 16 sonios y el nivel sonoro correspondiente será 80 fonios. Sin embargo, cuanto más próximas estén entre sí las frecuencias, mayor será su confluencia y la sonoridad total no tiene por qué ser la suma de las sonoridades individuales. En el caso extremo, el enmascaramiento producido por uno de los tonos puede ocasionar que otro de nivel inferior quede completamente inaudible.
Puede sorprender el hecho de que los tonos puros o de banda muy estrecha, prácticamente líneas espectrales puras, puedan tener influencia entre sí. Las investigaciones indican que los tonos puros excitan los nervios auditivos correspondientes a un campo amplio de frecuencias, lo que da origen al fenómeno del enmascaramiento.
La figura de la izquierda da idea de la banda de frecuencias afectadas por los tonos puros o de banda estrecha. En esta figura se representa el efecto enmascarante producido por un sonido puro de 400 Hz y 80 dB de nivel de presión.
ENMASCARAMIENTO.
En el tema 6, que versa sobre la exploración auditiva, hemos dedicado un capítulo al enmascaramiento y sobre todo a como utilizarlo en la exploración audiométrica. Para expresar matemáticamente la forma en que dos tonos puros excitan los nervios auditivos, en psicofísica se hace uso del parámetro denominado densidad sonora. Se entiende por tal el cociente de las diferenciales de la sonoridad y de la frecuencia tonal subjetiva.
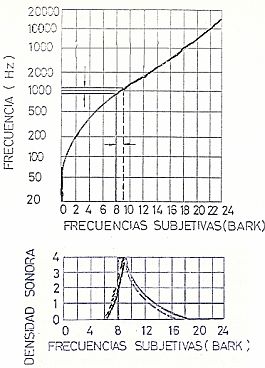
Densidad sonora =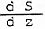 
= D S donde z es la frecuencia subjetiva medida en BARK. La relación entre la frecuencia tonal subjetiva y la frecuencia física viene dada en la figura de la izquierda.
La escala Bark es una escala psicoacústica. La escala tiene un rango del 1 al 24 y corresponde a las primeras 24 bandas críticas del oído. Los márgenes de las bandas son (en Hz) 0, 100, 200, 300, 400, 510, 630, 770, 920, 1080, 1270, 1480, 1720, 2000, 2320, 2700, 3150, 3700, 4400, 5300, 6400, 7700, 9500, 12000, 15500.
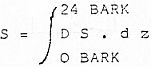
La sonoridad vendrá gráficamente reflejada por el área debajo de la curva de densidad, teniendo en cuenta que el intervalo audible está comprendido entre 0 y 24 BARK, la sonoridad será:
En la parte inferior de la figura de la izquierda se representa la función de densidad sonora para un tono de 1 KHz y 13 sonios. Se entiende por densidad sonora, o densidad de presión sonora, a la cantidad de energía por unidad de volumen. La altura del trazado continuo de esta figura muestra la densidad sonora de banda.
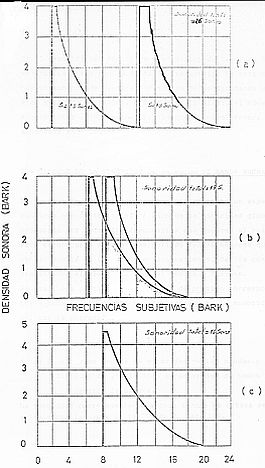La figura de la izquierda puede ayudar a entender el enmascaramiento mutuo entre dos tonos que representan tres situaciones de separación de frecuencias para dos tonos de la misma sonoridad individual, 13 sonios o lo que es lo mismo, 77 fonios.
En el caso (a) la distancia de las frecuencias es superior a 10 bandas críticas, no existiendo solapación de áreas. En este caso la suma de las sonoridades parciales dará la sonoridad global, es decir, la sonoridad global será 26 sonios.
En el caso (b) las áreas se solapan parcialmente dando una sonoridad inferior a la suma de las individualidades. Es lo que se conoce por enmascaramiento parcial. En el caso considerado la sonoridad conjunta es 19 sonios.
En el caso (c) los dos tonos caen dentro de la misma banda crítica, pero son de distinta frecuencia. En este caso hay un aumento de la densidad sonora de banda, dando un área total de 16 sonios, o lo que es lo mismo, el nivel sonoro total de 80 fonios, por lo que el nivel sonoro ha aumentado en 3 fonios.
SIMULACIÓN DE LA DISTRIBUCIÓN DEL ENMASCARAMIENTO EN LA MEMBRANA BASILAR.
La capacidad enmascarante de una componente determinada se distribuye por toda su banda crítica y por las de alrededor. Ambos modelos determinan el umbral de enmascaramiento de ruido para ambos tipos de componentes; para lograr esto, el modelo I compara con un enmascaramiento determinado empíricamente, mientras que el modelo II aplica una función de dispersión (FdD) que “dispersa” (extiende) la energía de una banda crítica hacia las que le rodean. Esta función de dispersión tiene forma constante en la escala bark (independiente de la frecuencia y del nivel del enmascarador), con pendientes de 25dB/Bark en la región de bajas frecuencias, y -10dB/Bark en la de altas frecuencias. En la banda crítica z se define por:
FdD(z) =15.81+ 7.5(z + 0.474) − 7.5[1+ (z + 0.474)2 ]0.5
Sólo se usan valores superiores a 60dB. El patrón de excitación en la membrana basilar viene dado por:
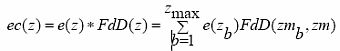
donde zm es el valor bark mediano de la partición z y zmax es el índice de partición mayor para la frecuencia de muestreo concreta. La impredecibilidad de cada partición también se convoluciona con la FdD para obtener:
como ct(z) está ponderada por la energía de la señal, se debe normalizar a cb(z) como:
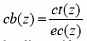
Idealmente, el efecto de la función de dispersión sobre la energía debe ser reversible. Implementándolo como un problema estándar de deconvolución pueden aparecer problemas numéricos como energías nulas o negativas en algunas regiones. Estos problemas aparecen por si solos dado que el proceso de deconvolución busca una solución estrictamente numérica que no tiene en cuenta las realidades físicas y acústicas de la situación. Por ello, se usa en su lugar un proceso de renormalización.
La función de dispersión, debido a su forma, aumenta la energía estimada en cada banda por los efectos de la dispersión. La renormalización tiene esto en cuenta y multiplica cada partición por el inverso de la ganancia de la energía, asumiendo una energía uniforme de 1 en cada partición. Como este no es el procedimiento más preciso, se da especial importancia a la aparición de un error muy pequeño en el proceso de estimación de la tasa de bit:
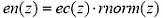
y el coeficiente de renormalización viene dado por:
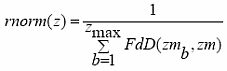
CÁLCULO DE LA SONORIDAD DE UN RUIDO DE BANDA ANCHA.
Los ruidos industriales presentan generalmente un espectro continuo que dificulta el cálculo de la sonoridad global producida por todas las frecuencias que componen el ruido. Para estos casos se han desarrollado varios métodos que tienen en cuenta el efecto de enmascaramiento, de los cuales presentamos el más simple que es debido a Stevens.
Se realiza a partir de los niveles de presión correspondientes a cada tercio de octava, determinándose la sonoridad global por la expresión:
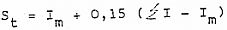
donde Im = máximo índice de sonoridad de las bandas y 
= suma de los índices de sonoridad de todos los tercios de octava.
La sonoridad correspondiente a cada tercio de octava se calcula con la ayuda de las tablas de niveles de presión sonora y sonoridad que pueden encontrarse en el capítulo 3 de este tema.
